Matt Stabeler

Met with Pádraig,  results so far are not complete, so we still need to:

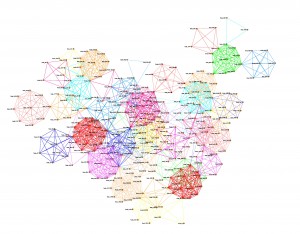
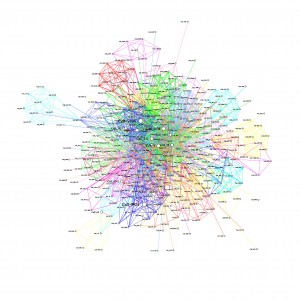
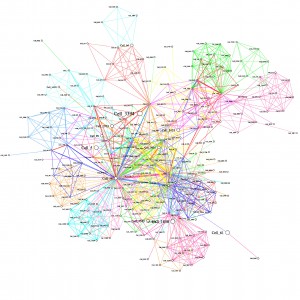
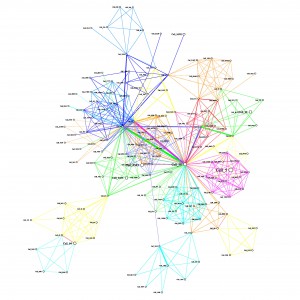
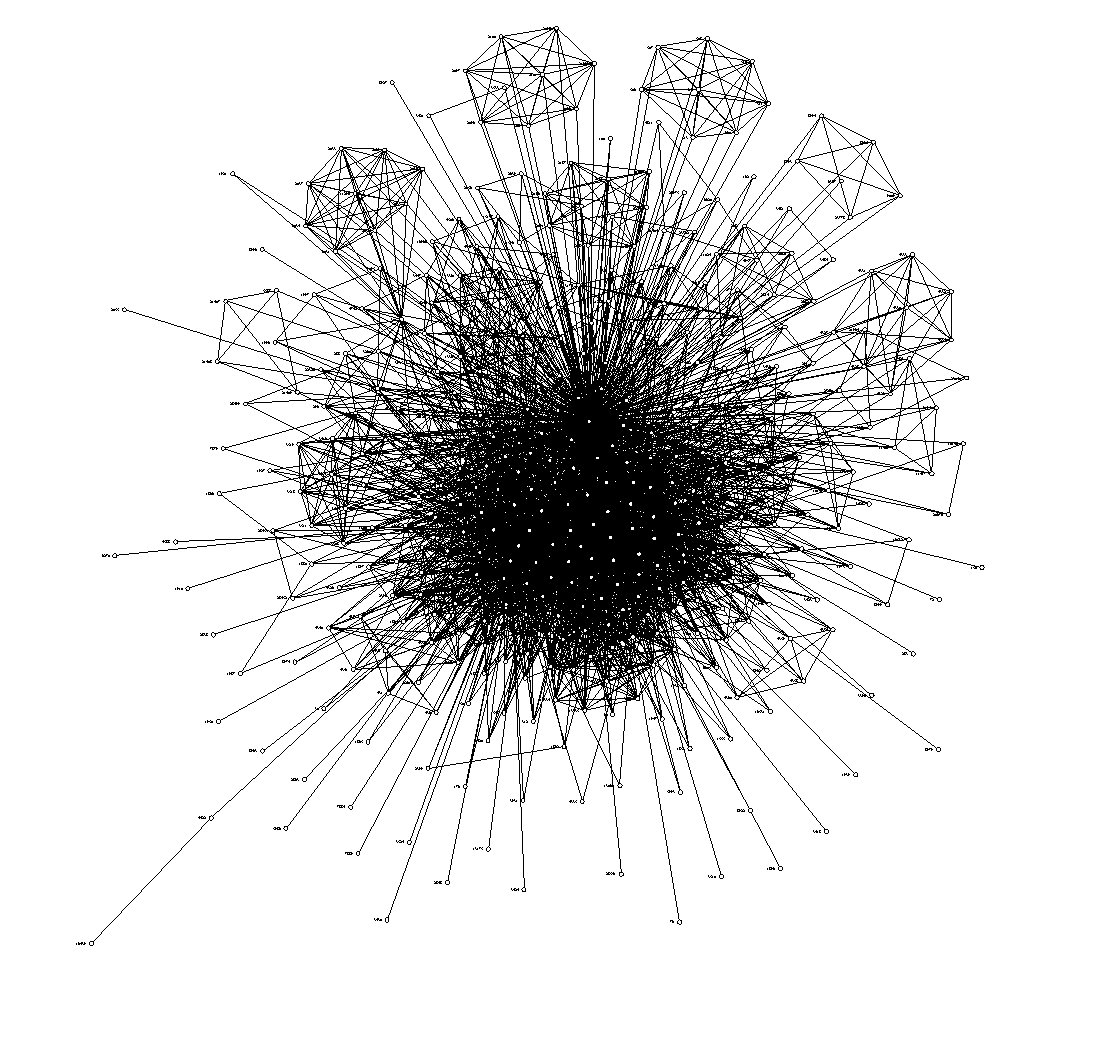
• Run routing based on ranked centrality only (i.e. the aggregate graph of all connections): Graham might have done this already. To give us a more complete picture of what routing towards the centre really looks like.
• Do more randomised ranking runs, to see of random can come up with better routing rank than LBR.
• Implement and test new LBR idea.

Next Step for LBR

Pádraig suggested a simple advancement for LBR:

Person A, has a  message for Person C, and has encountered Person B. A has to work out whether to pass the message on or not. Each node has  a probability matrix of visiting all locations at any time.

Probability matrix of nodes being at any given location

A makes his decision by calculating the dot product of his own locations against C’s locations, and comparing that to B’s calculation in relation to C. If the sum for the B.C is greater than A.C then A passes the message to B. The rationale being that when one encounters someone else, who is more likely to visit the same location as the destination person, then the message should be passed on, because they are more likely to see the other person.

There are some caveats….. TODO: buffer zone, future prediction, past history, recent(ness?), limited locations,

Some specific details/ideas/extensions to consider:

• We need to consider how these probability matrices will evolve over time. A nodes probability matrix will change when he/it visits new places, or alters existing mobility patterns. Initially, we can use the computed data, but more refined versions should exhibit a real-world scenario of unpredictable behaviour.
• Determine a good threshold to use, so that messages are not sent between people of very similar rank/score, the rationale being that there may not be a benefit in passing it on, and therefore try to reduce overhead.
• Limit the number of locations considered, to only those that are popular, this might boost the use of popular locations, in an attempt achieve a higher probability of a message being passed on.
• Consider a more sophisticated mechanism to predict co-location with the destination node, or a better conduit/carrier node, by predicting future interactions with nodes based on past history.
• It may also be important to show the possibility of real-world application, by implementing  a scheme for automatic dissemination and update of the probability matrix using the network itself. (related to  previous ideas about piggybacking meta-data using network/vector clocks, which themselves can be used as a source of routing metrics. e.g. recentness of contact, latency, update routes/speeds/times etc.)

Pádraig and I discussed the problems we may encounter in regards to peer review and justification of the work; in that the problem area is not well defined, and therefore we might have problems showing why this work is novel, and proving what our contributions are. To that end we need to explore the literature a little more, so we might be able to show a solid justification for the work, or alternatively, change our approach so it fits in better with other, better defined problems.

What sorts of messags are ‘delay tolerant’? Pádraig’s suggestion is that twitter messages, and facebook update messages might be delay tolerant, as a person may not need to receive all messages, and generally only want to get the latest updates, it does not matter if a few are lost along the way.

How do we define the urgency of messages, and the efficiency of the network? Perhaps one type of message can be delivered within 10 time periods, and still be considered to be relevant and within acceptable delivery time, but another message may need to be delivered within 1 time period, to ensure quality of service.

There is a categorisation issue too; where some messages can be considered one-to-one (direct messaging), some one-to-many (twitter update), many to many (local information) and many-to-one (sensor networks). We need to decide which of these we will consider. On this note, I said I would speak to Neil Cowzer, who is working on implicit group messaging, to see what his motivation is, and to see if he has a well defined problem space that he is tackling.

Another alternative that Pádraig suggested, was looking at social science approach, where we look at the heuristic approaches to routing in complex social networks. Pádraig’s suggestion was that on some networks, we might be able to apply certain routing techniques, which do not work on others. The contribution would be defining, categrorising and testing new and existing combinations of network types and routing mechanisms. This would be an interesting route to take, but would mean a step back in my research, as I would need to do reading into this area. This would link up well with the work of Stanley Milgram, Granovetter and Watts & Strogatz etc. So I should re-read some of this work, but more importantly, take a look at the biggest cited, citing documents, to see where research might be heading now.

Had a meeting with Pádraig; we discussed using MOSES to get the list of communities of cell towers.

To recap, two cell towers are linked, if during a contact (Bluetooth) between two people, they are spotted by either person. This generates a huge furball of when visualised. I installed MOSES on a server, and ran it on the graph generated from MIT Oct 2004. It produced 66 Communities. There are 468 nodes in the dataset. The average number of communities per node is 2.17.

Padraig suggested visualising the data, and colouring each community in turn, so that we might be able to get an idea about which communities we can remove (as they are too big), and will leave us with smaller subsets of the graph, which identify locations better.

We can then use these communities as the ‘locations’ in location based routing. We need to determine whether it matters if a node report multiple ‘locations’ at the same time.

I started to view the communities colours as suggested, but it still showed a very large furball, so I decided to see what happenned when the highly connected nodes are removed. In the image below, we can see that when the top  100 highly connected nodes are removed, it becomed clear that there are distinct groups of cell towers.

MIT Oct 2004, when two users see each other, the cell towers they see are linked. This version has the top 100 highest connected (degree) nodes removed. Edges show community membership as given by MOSES.

I sent on the moses output, and list edges to Aaron McDaid and Daniel Archambault, who genereated the Euler diagram  below using Tulip.

the layout in the visualization is based solely on the communities found by moses. Tulip attempts to lay out the sets in an Euler diagram such that communities are placed nearby if they share nodes in common.

Euler Diagram generated using Tulip from the output of MOSES for cell towers connected in MIT Oct 2004.

I have yet to speak to Aaron in more detail about what this diagram means, but if I have interpreted the visualization correctly, the similar coloured areas are collections of nearby nodes; seperated into distinct clusters, rather than overlapping ones. If it is possible to extract this clustering, it might provide exactly the location clustering we need, if we remove the very large clusters (light brown/green).

I took some time to review the way that cell towers are linked, to make sure that it was making a fair linking, ready for when MOSES did it’s thing. As it is, it is a little loose in how it determined whether two cells are linked, as it links all cells that are seen in an entire contact period. This means that cells that are linked when two people are travelling together. I plan to work on a more strict approach, where the duration of the cell sightings for each person are compared, and cells linked only when it is clear that they are at the same time. However, I continued using the results we already have.

The images below show the graphs, when the top N communities are removed. The size of the node relates to the number of times a cell tower is reported, using binning.

The most number of times a node is spotted is 9291, the smallest is 1, so
9291 - 1 / 10 bins = bin size of 929.
For example, if a node is spotted 1043 times, then it will be placed into bin 2.

The width of the edge relates to the number of times an edge is reported between its two vertices, again using binning. The most number of times an edge is spotted is 3676, minimum 1. The average however, is only 8.38, and the median is only 3, so the binning really only distinguishes the very highly seen nodes.

The colour of the edges is related to the community membership. Because nodes can be members of multiple communities, and therefore have multiple edges, I made the decision to create only one edge, and distinguish it using the concatenation of the community names (e.g. Community_0Community4…), so nodes that edges that make up the same communities, will have the same colour. This might not have been the best way to do it, but the software used does not show multiple edges between the same nodes. An alternative would be to make the width of the edge equal to the number of communities it represents.

Minus 1 Community

Minus 15 Communities

Minus 30 Communities

Minus 40 Communities

As communities are removed, the graph becomes clearer, where 40 communities are removed, it becomes more obvious that there are distinct communities and the high degree nodes are more obvious.

eps and png files for other numbers removed

The goal is; given any cell tower id, we can identify which community it belongs to, and by extension, the ‘location’ the node is at.

An idea I have for finally making this data usable, so that we have distinct communities. Ignore the top N communities (e.g. 30). Order each community by summed weight of edges, then take the highest degree node, and assign it to the community it belongs to, that has the highest rank, then remove that node from further consideration. Continue until all nodes are assigned to a community. This may need some more thought.

I processed the contact logs, rather than just the hop logs, and after ~6 hours it completed! Now all contacts in the whole MIT dataset have associated cell towers. If a cell tower could not be found for the contact duration, then a second search was done for a record of a cell tower finishing  in the previous hour. The timestamps are preserved so that they can be excluded later. The following shows the stats for this data, in regards to cell towers.

Row Count:	114046

Both Have Cells:		28804	 (25%)
Neither have cells:		34587	 (30%)
One side has cells:		50655	 (44%)
	From has cells:		30557	 (27%)
	To has cells:		20098	 (18%)
Nodes share cell:		4045	 (4%)
First start time:		Thu, 01 Jan 2004 04:03:17 +0000
Last end time:			Thu, 05 May 2005 03:39:29 +0100

This means that out of 114046 contacts between 01 Jan 2004 and 05 May 2005, only 4045 nodes report at least one cell in common at time of contact, but 28804 report different cells, and a further 50655 report cells for at least one of the nodes. This means, that if we assume that a one sided cell sighting at time of contact determines a cell sighting for both nodes, then we have cell towers for ~73% of  contacts.

The assumption is that if any of the cell towers seen in the contact period, then the nodes are considered to share a cell. However, this can be further refined if needs be, to be more strict, where a contact period is very long.

UPDATE:
Below is a visualisation of the connected cell towers for MIT-Oct 2004, it it very confused and has a huge central mass, but there are clear connections of towers on the periphery. I think this can be further refined to be more strict about cell tower connections (as at the moment, the dataset contains more than 1 cell tower for any given contact period). Also, at the moment it links two cells even when two nodes are on contact for a long period of time, in which they could conceivably be moving together.

Cell towers where an edge is made when either node in a contact event has seen one of the cell towers.

In the last meeting I had with Pádraig we went through the spectral clustering technique, and discovered that there were some errors in my calculations of the the clusters. I took the time to re-do the community calculations,  and to run the tests again, to make sure all is correct. I used the MIT  dataset, and constrained it to the month of October 2004 (as before). Messages are created and initially sent at the first time step. The selected communities for each week are taken as the biggest group, which in practice were roughly the same set of connected nodes. I chose to omit the nodes with a value of 0.0 in the matrix (V) (see  data pipelines).

Delivery Ratio over time

This plot shows the delivery ratio over time for MIT-OCT dataset, for LBR communities (where the community is taken from weeks 1, 2, 3, 4 and all 4 weeks), PBR, Prophet, Unlimited Flood and Random(1.0, 0.2, 0.0).

Final Delivery Ratio and Cost

This chart shows delivery ratio and cost for each Protocol, note that unlimited flood does not report cost.

In these updated plots, it is encouraging to see that with the corrected community structure, LBR actually performs well, and in fact for the community structure in week 1, it performs better overall than PBR, with weeks 2, 3, 4, all, close behind. It is also good to see that LBR is beating Random 0.0, and 0.2 consistently. LBR week 1 Community also tracks a small way behind Flooding for a short while around 05/10 – 08/10 which is quite interesting. The communities are listed below (or can be viewed here), for further analysis.

UPDATE:

Having given this a little more thought, this is a little mis-leading, so I have generated new plots where all Protocols are constrained to the same community nodes. Unfortunately, this yields a similar spread of results between the protocols, as did the results that did not consider community structure. Only the structure discovered in week 1 increases the delivery ratio.

Delivery Ratio for each community, for each protocol

This plot shows delivery ratios for each community generated from different weeks and all weeks in Oct 2004 for the MIT Reality Mining dataset

This shows the final delivery ratios and costs for each protocol, for MIT OCT 2004, communitites

What I plan to do now is to go back to the ranking algorithm, and use the linked cells mechanism to re-calculate the rankings. It might also be useful to start thinking about being able to use the real-time location information (in this case cell towers/linked cell towers) in a routing algorithm directly. This would let us start to implement some simplistic location predictions.

I also created a clearer graph visualisation for the cell tower links, this shows that there is a componant that  encompasses a large percentage of the reported cells overall. If we were to consider this one location, it is possible that it covers a very large area.

This shows the cell towers that are connected when at least 100 messages are passed and reported at both cell towers, edges are numbered where this is more than 300.

Using the log of hop events, I was able to generate a list of cell towers being used at the time of the hop, from this I built a list of the cell towers that are linked in this way, with a count of the number of times they had been connected (linked_cell list txt, or linked_cells json version ). From this a created a graph where the weight of the edges is the count.

Edges with a weight (or number of times nodes passed a message and reported different cell towers) less than 100 are removed for clarity, the colour of the edges shows the weight of the edge increasing from blue to green.

The tool that I have used to visualise these graphs is called the network workbench, and it reports the following about the graph:

Nodes: 84
Isolated nodes: 9
Node attributes present: label
Edges: 149

No self loops were discovered.
No parallel edges were discovered.
Edge attributes:
Did not detect any nonnumeric attributes
Numeric attributes:
min    max    mean
weight     1    2700    103.42953

This network seems to be valued.

Average total degree: 3.547619047619045
Average in degree: 1.7738095238095228
Average out degree: 1.7738095238095228
This graph is not weakly connected.
There are 14 weakly connected components. (9 isolates)
The largest connected component consists of 67 nodes.
This graph is not strongly connected.
There are 61 strongly connected components.
The largest strongly connected component consists of 24 nodes.

Density (disregarding weights): 0.02137
Additional Densities by Numeric Attribute
densities (weighted against standard max)
weight: 2.21041
densities (weighted against observed max)
weight: 0.00082

Edges are coloured linearly from white to black depending on weight, edges with a weight greater than 300 are labelled.

It seems that there are is a group of towers that are strongly connected, by large number of messages being passed, and nodes reporting them as being the cell towers used. One possible reason for this,  is perhaps because the places where the nodes are, are popular, and as such, require more cell towers to cover the demand. These results are promising, because it means that if we pre-process the data, and ignore connections where there is a low weight, we can use groups of towers to give a notion of place. What this means is, when a node reports a tower in the known cluster of towers, we can assume that it is in roughly the same place as any other node who also reports a tower in the same cluster.

I calculated the communities as described  in data-pipelines and from this generated two lists of nodes for every week in October, and for all weeks.  I took the largest list for each, and used that as the community for which to test the LBR algorithm.

Updated plot, showing the delivery ratio for LBR-Community, one (dotted) line for the communities found in each week, and overall.

It seems that, as expected, routing within the community gives an advantage to the algorithm, and in fact, when the community knowledge is derived from the full dataset, then LBR performs better that the average of the rotated dataset. This plot is slightly misleading however, as the data for the previous algorithms is the rotated averages, whereas the data for LBR-Community is for straight runs. Below is the plot against straight runs of each other algorithm.

This plot shows straight runs of all algorithms, and the updated LBR-Community runs.

In this plot, it is obvious that the difference is less profound as with the average plots, however, I am considering running the rotation scheme again for LBR-Community.

Met with Pádraig and Davide briefly to discuss the poor performance of the LBR algorithm. Pádraig had previously suggested that we run multiple simulations over different time slots, and Davide and I had talked about and planned to do split the runs up as follows:

Measuring the delivery ratio, and cost for PBR, LBR, Prophet, Random 1.0, Random 0.2,  Random 0.0 and Flooding, will give us a good picture about the nature of the data, and we will be able to see if the previous plots are representative of the data.

I will also try to adapt the ranking mechanism, to include only the top (most seen) 10% or 20% of cell towers, to see if that makes any difference to the results.

Update:
Using the method above, I ran the simulations for LBR, PBR, Unlimited Flood, Random 1.0,0.0,0.2 and Prophet. Below is the average delivery ratio over 18 runs, for each  protocol in 28 day time windows, at 7 day intervals,  between  27 Aug 2004 and 21 Jan 2005.

Average delivery ratio over 18 runs for each protocol, between Aug 2004 and Jan 2005

There does seem however, to be a few issues with the number of lines returned in the logs, this suggests that somehow, I have mis-calculated, probably just for the end  time period used, the start and end time period, but this seems to only account for the last few hours of each run (out of the month). So until I find the error, I think these results are roughly correct.

Using the simple formula for calculating the ranking of users, as follows:

Popularity of user [latex]i = \sum_j \tau_{ij} ( p_j )[/latex]
where [latex]\tau_{ij}[/latex] is the time (or number of times) user [latex]i[/latex] has visited the tower [latex]j[/latex], [latex]p_j[/latex] is the popularity of tower [latex]j[/latex].

Create a list of towers, with an associated number of times the tower is reported in the dataset, call this the set [latex]p[/latex],

SELECT count(celltower_oid) as count, celltower_oid FROM cellspan GROUP by celltower_oid ORDER BY count DESC

then for each user, get a list of the cell towers, with an associated number of reading for that user, and call this set  [latex]\tau[/latex]

SELECT count(celltower_oid) as count, celltower_oid FROM cellspan WHERE person_oid = {USER_ID} GROUP by celltower_oid ORDER BY count DESC

then, for each member of  [latex]\tau[/latex], multiply the number of time the tower is seen in  [latex]\tau[/latex]  by the number of time the tower is seen in total from  [latex]p[/latex].

This yields a number for each user, which can be used when initialising nodes in ContactSim (aka LocationSim). I added new properties into the the configuration files, which reflected the ranking of each node, and created new classes in LocationSim, which reflected a new protocol called LBR. When a node is instantiated, is looks up its ranking metric with an oracle class (which reads the data from the configuration file). During the operation of the simulator, when a node get’s an onConnect() event call, it checks it messages to see:

1. if it has any message for the node it is connected to, it passes them on
2. if the node it is connected to has a higher ranking, then it passes all messages on

The initial results show a good delivery ratio compared to PBR

Delivery COST of messages for LBR and PBR using 7 day periodicity, where messaging starts at the first timestep (PBR 7 day Period Start, LBR Start), or after 1 week.

Delivery Ratio of messages for LBR and PBR using 7 day periodicity, where messaging starts at the first timestep (PBR 7 day Period Start, LBR Start), or after 1 week.

This suggest that simply knowing the rank of the users, based on location, significantly improves routing. However, I need to check the algorithm is working before I can say the results are accurate:

• Does the node remove it from it’s buffer when it passes the message on? Yes it does
• Is the node correctly recording deliveries?

Currently working on: Graph of all connected users. Taking a long time……

I have had a chance to look at the code that Derek sent me, namely the CFinder software for finding k-Cliques, and an implementation of the MDS  algorithm, I struggled to get these to make any sense of the data that I have, and started to think about an alternative approach.

Despite the decision we made in a previous meeting, to consider location readings globally, regardlessof order/time, I decided to consider using the nature of the data to inform the clustering algorithm, namely, using the time ordering to indicate the relationship between readings. This meant going back to the idea of using readings from  individuals, to determine the places that are relevant to them. This of course may have issues when comparing places from different individuals, but no more than when implementing a simulator (or real world) system, where individuals track their own movement patterns.

By taking time ordering into consideration, we can implicitly detect when a node is moving from one place to another, by measuring the distance between the current reading, and the centroid of previous readings from a known place.

- take each location reading for a person, and measure the distance
            between it and the center of the current cluster
    - if the distance of reading from the center of current cluster is greater
        than the mean distance of points in the cluster to the center + alpha,
        then it is outside of the cluster.
        - read ahead by X (to make sure this is not just an erroneous reading)
        - if X readings are beyond the threshold of Current cluster
          - then we have left the location,
              - record the current cluster if it has more than
                  N location readings
              - start a new cluster with the current reading
        - else
          - discard the erroneous reading
    - else
      - add to list of cluster points
      - re-calculate cluster centre

Where alpha is a metric that allows the cluster to grow, alpha can be fixed (say 50m) or a function of the mean distance to the centre of the cluster. The number of readings to read ahead (X) should probably be fixed at say, 10, so that if the person goes away and comes back very quickly, they are considered to have not left.

The minimum number of readings required to consider a cluster valid should be relatively large, say 10 or 20, so that only places where the user lingers for some time, are considered. If we use a number too high, then we will miss some important places. A number too small would mean that places where users just pause for a while will be recorded, which may not be important places.

The algoritm still need improvement, so that it also considers the time between readings; for example, rather that considering the number of readings in a cluster, consider the amount time between the first and most recent reading, and use this to determine whether a place is recorded. This means that we should be able to record important places even if readings were not taken for some reason.

In the last post, I described a method for deciding on co-location based on spotting of common WiFi points, which co-located users if they saw the same WiFi access point, at roughly the same time. We refined this method to discriminate when the approximate distance, based on signal reading (which could be signal strength, or signal quality). Pseudo code for this algorithm:

• For each consecutive timestep window, between start and end.
  • Retrieve all readings within that window for all users.
    • Foreach user
      • pick the strongest signal from the list of readings for each access point (as there may be multiple)
      • rank reading in order if signal strength
      • discard the readings for access points where:
        • Signal Strength divided by Strongest Signal Strength is less than Alpha
      • Foreach other user
        • perform signal processing as above
        • if the intersection of the remaining list of access points for each user is not null, consider the two to be co-located

The variables in this algorithm are the start and end time, the size of the window and the alpha value.

There were a few factors to consider before we could implement this, firstly, it was important to find out what the values for signal strength actually meant;  the data ranged between values of 11 to 110.  I used an N95 phone, with the Campaignr software installed, to record a number of reading at varying distances from known access points. I instructed the software to upload to a script that simply recorded the data in a text file.  This showed that the ‘signal_strength’ value increases as the phone moves away from the access point. Another factor to consider, was the range of values that were reported in the database. Davide suggested plotting the values of all signal strengths for all readings, over the the readings that would be selected using the alpha value selection. The figure below shows the data based on an alpha value of 0, for all readings,  0.8, and 1.0 (for only the strongest readings).

The second figure shows all readings, split into individuals.

The next step is to decide what alpha value to use, and store the co-locations into the database. To this end, I have written a script to parse all 3.6 million records, calculate the alpha value (Strongest signal strength over signal strength) and write the value back into the database. This will allow us to quickly see the effect of using different alpha values for decision making, without having to repeat the calculations every time.  It will also allow us to plot the effect of different alpha values against each other very quickly.