Matt Stabeler

We discussed the results so far, and I suggested there was scope to improve the global ranking used by BubbleRAP, Pádraig hatched upon a clever idea to use hierarchical clustering to drive routing. Pádraig invited Conrad in to tell us about how Hierarchical GCE works. He descbibed how it will give some notion of stable heirararchical denodograms cut-points.

We then discussed the idea of causing the global routing part of BubbleRAP to use this hierarchy, by selecting only the minimum set of  communities that contain the destination node for routing to. In the example above, routing from C to P would mean using the top level community. However, a route between F and A, would mean not passing messages to communities encompassed by N, M, O and P, as they are not in the minumum set. The thinking behind this, is that we can prevent messages being sent to obscure places in the network, and thus reduce overhead, and perhaps increase delivery latency.

One possible criticism, is that this might be hard to justfify in terms of reality, as nodes will not be able to have pre-computed community knowledge. Conrad mentioned that he had been working on some ideas regarding vector clocks, which might be applicable, as I have said before, we could use some data within the vector clocks as metric for routing, and also use it as a means of communicating network structure data, so that each node can calculate the state of the network based on it’s knowledge, and therefore a clever mechanism to label communities could be devised which would allow nodes to route based on this hierarchical knowledge.

Conrad will hook me up with the code to do the clustering, and I will work out how to implement this in the simulator.

Met with Pádraig,  results so far are not complete, so we still need to:

• Run routing based on ranked centrality only (i.e. the aggregate graph of all connections): Graham might have done this already. To give us a more complete picture of what routing towards the centre really looks like.
• Do more randomised ranking runs, to see of random can come up with better routing rank than LBR.
• Implement and test new LBR idea.

Next Step for LBR

Pádraig suggested a simple advancement for LBR:

Person A, has a  message for Person C, and has encountered Person B. A has to work out whether to pass the message on or not. Each node has  a probability matrix of visiting all locations at any time.

Probability matrix of nodes being at any given location

A makes his decision by calculating the dot product of his own locations against C’s locations, and comparing that to B’s calculation in relation to C. If the sum for the B.C is greater than A.C then A passes the message to B. The rationale being that when one encounters someone else, who is more likely to visit the same location as the destination person, then the message should be passed on, because they are more likely to see the other person.

There are some caveats….. TODO: buffer zone, future prediction, past history, recent(ness?), limited locations,

Some specific details/ideas/extensions to consider:

• We need to consider how these probability matrices will evolve over time. A nodes probability matrix will change when he/it visits new places, or alters existing mobility patterns. Initially, we can use the computed data, but more refined versions should exhibit a real-world scenario of unpredictable behaviour.
• Determine a good threshold to use, so that messages are not sent between people of very similar rank/score, the rationale being that there may not be a benefit in passing it on, and therefore try to reduce overhead.
• Limit the number of locations considered, to only those that are popular, this might boost the use of popular locations, in an attempt achieve a higher probability of a message being passed on.
• Consider a more sophisticated mechanism to predict co-location with the destination node, or a better conduit/carrier node, by predicting future interactions with nodes based on past history.
• It may also be important to show the possibility of real-world application, by implementing  a scheme for automatic dissemination and update of the probability matrix using the network itself. (related to  previous ideas about piggybacking meta-data using network/vector clocks, which themselves can be used as a source of routing metrics. e.g. recentness of contact, latency, update routes/speeds/times etc.)

Pádraig and I discussed the problems we may encounter in regards to peer review and justification of the work; in that the problem area is not well defined, and therefore we might have problems showing why this work is novel, and proving what our contributions are. To that end we need to explore the literature a little more, so we might be able to show a solid justification for the work, or alternatively, change our approach so it fits in better with other, better defined problems.

What sorts of messags are ‘delay tolerant’? Pádraig’s suggestion is that twitter messages, and facebook update messages might be delay tolerant, as a person may not need to receive all messages, and generally only want to get the latest updates, it does not matter if a few are lost along the way.

How do we define the urgency of messages, and the efficiency of the network? Perhaps one type of message can be delivered within 10 time periods, and still be considered to be relevant and within acceptable delivery time, but another message may need to be delivered within 1 time period, to ensure quality of service.

There is a categorisation issue too; where some messages can be considered one-to-one (direct messaging), some one-to-many (twitter update), many to many (local information) and many-to-one (sensor networks). We need to decide which of these we will consider. On this note, I said I would speak to Neil Cowzer, who is working on implicit group messaging, to see what his motivation is, and to see if he has a well defined problem space that he is tackling.

Another alternative that Pádraig suggested, was looking at social science approach, where we look at the heuristic approaches to routing in complex social networks. Pádraig’s suggestion was that on some networks, we might be able to apply certain routing techniques, which do not work on others. The contribution would be defining, categrorising and testing new and existing combinations of network types and routing mechanisms. This would be an interesting route to take, but would mean a step back in my research, as I would need to do reading into this area. This would link up well with the work of Stanley Milgram, Granovetter and Watts & Strogatz etc. So I should re-read some of this work, but more importantly, take a look at the biggest cited, citing documents, to see where research might be heading now.

Had a meeting with Pádraig; we discussed using MOSES to get the list of communities of cell towers.

To recap, two cell towers are linked, if during a contact (Bluetooth) between two people, they are spotted by either person. This generates a huge furball of when visualised. I installed MOSES on a server, and ran it on the graph generated from MIT Oct 2004. It produced 66 Communities. There are 468 nodes in the dataset. The average number of communities per node is 2.17.

Padraig suggested visualising the data, and colouring each community in turn, so that we might be able to get an idea about which communities we can remove (as they are too big), and will leave us with smaller subsets of the graph, which identify locations better.

We can then use these communities as the ‘locations’ in location based routing. We need to determine whether it matters if a node report multiple ‘locations’ at the same time.

I started to view the communities colours as suggested, but it still showed a very large furball, so I decided to see what happenned when the highly connected nodes are removed. In the image below, we can see that when the top  100 highly connected nodes are removed, it becomed clear that there are distinct groups of cell towers.

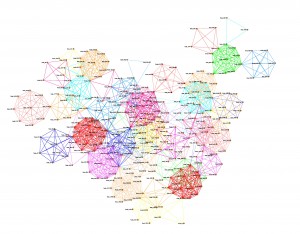
MIT Oct 2004, when two users see each other, the cell towers they see are linked. This version has the top 100 highest connected (degree) nodes removed. Edges show community membership as given by MOSES.

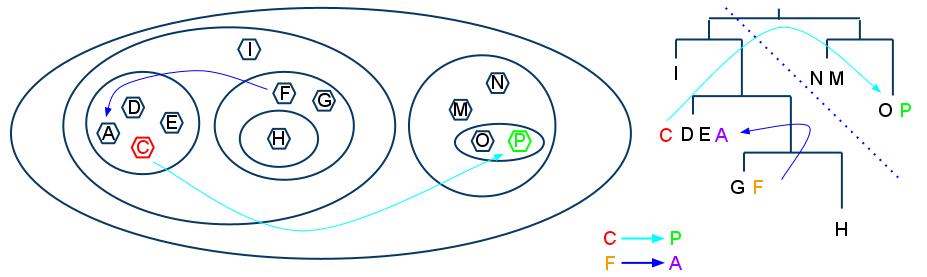
I sent on the moses output, and list edges to Aaron McDaid and Daniel Archambault, who genereated the Euler diagram  below using Tulip.

the layout in the visualization is based solely on the communities found by moses. Tulip attempts to lay out the sets in an Euler diagram such that communities are placed nearby if they share nodes in common.

Euler Diagram generated using Tulip from the output of MOSES for cell towers connected in MIT Oct 2004.

I have yet to speak to Aaron in more detail about what this diagram means, but if I have interpreted the visualization correctly, the similar coloured areas are collections of nearby nodes; seperated into distinct clusters, rather than overlapping ones. If it is possible to extract this clustering, it might provide exactly the location clustering we need, if we remove the very large clusters (light brown/green).

I took some time to review the way that cell towers are linked, to make sure that it was making a fair linking, ready for when MOSES did it’s thing. As it is, it is a little loose in how it determined whether two cells are linked, as it links all cells that are seen in an entire contact period. This means that cells that are linked when two people are travelling together. I plan to work on a more strict approach, where the duration of the cell sightings for each person are compared, and cells linked only when it is clear that they are at the same time. However, I continued using the results we already have.

The images below show the graphs, when the top N communities are removed. The size of the node relates to the number of times a cell tower is reported, using binning.

The most number of times a node is spotted is 9291, the smallest is 1, so
9291 - 1 / 10 bins = bin size of 929.
For example, if a node is spotted 1043 times, then it will be placed into bin 2.

The width of the edge relates to the number of times an edge is reported between its two vertices, again using binning. The most number of times an edge is spotted is 3676, minimum 1. The average however, is only 8.38, and the median is only 3, so the binning really only distinguishes the very highly seen nodes.

The colour of the edges is related to the community membership. Because nodes can be members of multiple communities, and therefore have multiple edges, I made the decision to create only one edge, and distinguish it using the concatenation of the community names (e.g. Community_0Community4…), so nodes that edges that make up the same communities, will have the same colour. This might not have been the best way to do it, but the software used does not show multiple edges between the same nodes. An alternative would be to make the width of the edge equal to the number of communities it represents.

Minus 1 Community

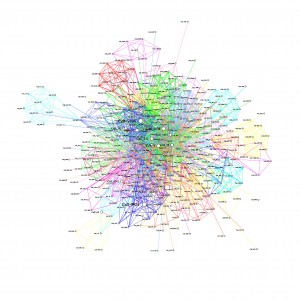
Minus 15 Communities

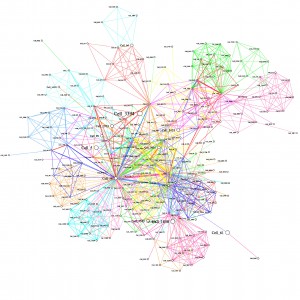
Minus 30 Communities

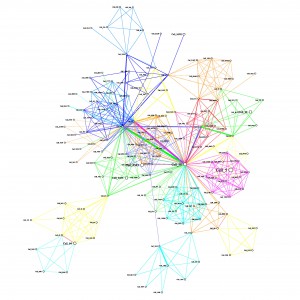
Minus 40 Communities

As communities are removed, the graph becomes clearer, where 40 communities are removed, it becomes more obvious that there are distinct communities and the high degree nodes are more obvious.

eps and png files for other numbers removed

The goal is; given any cell tower id, we can identify which community it belongs to, and by extension, the ‘location’ the node is at.

An idea I have for finally making this data usable, so that we have distinct communities. Ignore the top N communities (e.g. 30). Order each community by summed weight of edges, then take the highest degree node, and assign it to the community it belongs to, that has the highest rank, then remove that node from further consideration. Continue until all nodes are assigned to a community. This may need some more thought.

Presentation summary:

Routing in Human Interaction Networks

The goal of this seminar is to get some ideas from the participants, about the feasibility, and possible directions for this research.

We believe that by detecting the underlying patterns of human interaction involving movement and contacts between individuals, we can design a delay tolerant mechanism for passing messages between actors in the system (for example using mobile phones) that does not rely on fixed infrastructure. A system such as this should exhibit low cost (hop count, update overhead, delivery latency) and high efficiency (delivery ratio).

We believe that we can drive a routing policy by calculating and sharing metrics and meta-data at node level; from the contacts they make and the places they visit, without the need for a centralised system. In particular we are interested in using location to drive the messaging scheme.

We will show recent, related results of Persistence Based Routing vs existing schemes, some initial results from our simple schemes, and will ask for suggestions regarding the direction of our research into Location Based Routing.

Present: Pádraig Cunningham, Davide Cellai, Derek Green, Conrad Lee, Fergal Reid, Neil Hurley

Presented some background, and ideas about routing in human interaction networks (Slides – 1.2MB), someone noted tha Delivery Ratio and Latency are directly linked, with the suggested that the requirement for high delivery ratio and low latency, may not be intuitive in some situations. e.g. when someone who will cause a high latency, may be the only one to get the message across.

The presentation seemed to go well, however some parts I might not have delivered properly, meaning that I seemed to be skimming over a few bits.

Some suggestions were made:

• Consider the use of some sort of altered vector clocks, which keep a history, and can be shared with other nodes
• Partition the graph in the Reality Mining data, to identify the communities, then test the algorithms for only those communities
• Strong consensus to start using periodic patterns for predicting routes
• Neil suggested that I try to generate a dataset that does work well for LBR
• Ferhgal suggested what we had talked about before: finding out at what places, messages get sent

Reference to chase up:

1. PNAS 2005/2006 – LIBEN-NOWELL – ?GeoRouting in social networks?
2. SneakerNet
3. Talk to Martin Harrigan – who is using Vector Clocks in some clever way

There may have been other things I don’t remember – feel free to comment with additions!